
Tablas de valores
Una tabla es una representación de datos, mediante pares ordenados, expresan la relación existente entre dos magnitudes o dos situaciones.
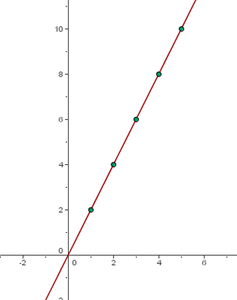
La siguiente tabla dos muestra la variación del precio de las patatas, según el número de kilogramos que compremos.
| Kg de patatas | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Precio en € | 2 | 4 | 6 | 8 | 10 |
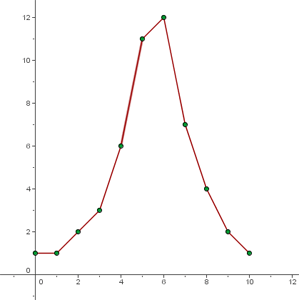
La siguiente tabla nos indica el número de alumnos que consiguen una determinada nota en un examen.
| Nota | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nº de alumnos | 1 | 1 | 2 | 3 | 6 | 11 | 12 | 7 | 4 | 2 | 1 |
Representación gráfica
Una gráfica es la representación en unos ejes de coordenadas de los pares ordenados de una tabla.
Las gráficas describen relaciones entre dos variables.
La variable que se representa en el eje horizontal se llama variable independiente o variable x.
La que se representa en el eje vertical se llama variable dependiente o variable y.
La variable y está en función de la variable x.
Una vez realizada la gráfica podemos estudiarla, analizarla y extraer conclusiones.
Para interpretar una gráfica, hemos de observarla de izquierda a derecha, analizando cómo varía la variable dependiente, y, al aumentar la variable independiente, x.
| Kg de patatas | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Precio en € | 2 | 4 | 6 | 8 | 10 |
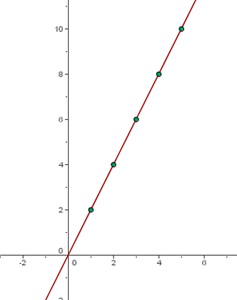
En esa gráfica podemos observar que a medida que compramos más kilos de patatas el precio se va incrementando.
| Nota | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Nº de alumnos | 1 | 1 | 2 | 3 | 6 | 11 | 12 | 7 | 4 | 2 | 1 |
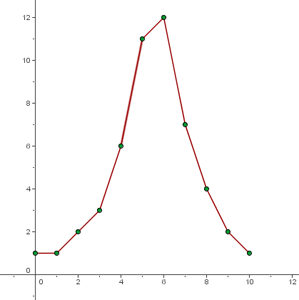
En esta gráfica observamos que la mayor parte de los alumnos obtienen una nota comprendida entre 4 y 7.
Características de las gráficas
Gráfica creciente
Una gráfica es creciente si al aumentar la variable independiente aumenta la otra variable.
Gráfica decreciente
Una gráfica es decreciente si al aumentar la variable independiente disminuye la otra variable.

Gráfica constante
Una gráfica es constante si al variar la variable independiente la otra permanece invariable.

Una gráfica puede tener a la vez partes crecientes y decrecientes.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
Hola con gusto lo haremos, pero podrías señalar en que ejercicio quieres que lo hagamos, para poder ayudarte.
Podrían mostrar los pares ordenados para graficarlo, gracias