Capítulos
El concepto de función es uno de los más importantes tanto en Matemáticas, como en Física, Química, Medicina, Estadística, Economía, Ingeniería, Psicología, entre otras. Y probablemente te has preguntado cuales serían ejemplos de funciones en la vida cotidiana.
Al pensar en ejemplos de funciones en la vida cotidiana podemos pensar en una máquina expendedora, ya que uno ingresa un código y la maquina te regresa un producto, el llamar por teléfono también es un ejemplo de una función, tu ingresas un número y se te conecta con el otro teléfono.
Hay muchos más ejemplos como estos que puedes encontrar en tu día a día usando el concepto de función que te presentamos a continuación.
Concepto de función
Una función es una relación entre dos magnitudes, de tal manera que a cada valor de la primera (conocida como dominio) le corresponde un único valor de la segunda (llamada imagen).
Ejemplos de funciones
1Un ejemplo habitual de función numérica es la relación entre la posición y el tiempo en el movimiento de un cuerpo.
Supongamos que un automóvil se desplaza con una aceleración de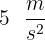 
recorre una distancia 
que está en función del tiempo transcurrido 
.
La función matemática que describe la distancia que recorre el automóvil al tiempo está dada por la expresión: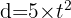
Podemos crear una tabla de los valores de las variables, anotando la distancia recorrida en un cierto instante de tiempo , para varios momentos distintos:
| t | 0.447 | 0.632 | 0.774 | 0.894 |
|---|---|---|---|---|
| d=5 t^2 | 1 | 2 | 3 | 4 |
De igual forma podemos representar gráficamente la posición del automóvil de la siguiente manera:
En estos casos se dice que es la variable dependiente (ya que depende del valor de ) y la variable independiente.
2Viaje en taxi.
Supongamos que el precio de un viaje en taxi viene dado por:
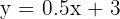
Donde 
representa el precio final (variable dependiente), 
la distancia en km que dura el viaje (variable independiente) y el 
corresponde al valor impuesto para asegurarse que un número bajo de kms pueda ser rentable para el chofer.
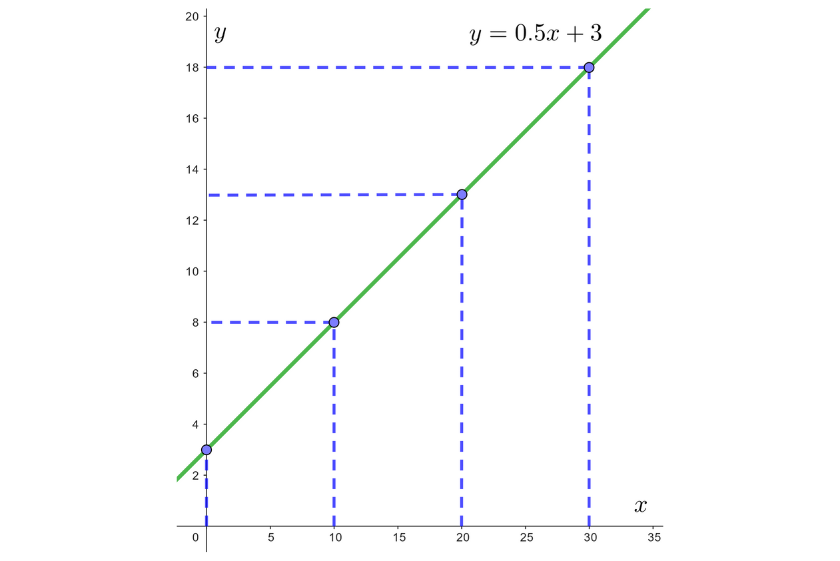
Podemos crear una tabla de los valores de las variables, anotando el precio del viaje a cierta distancia , para distintas distancias:
| x | 0 | 10 | 20 | 30 |
|---|---|---|---|---|
| y=0.5x+3 | 3 | 8 | 13 | 18 |
De igual forma podemos representar gráficamente la posición del automóvil de la siguiente manera:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
El Punto de inflexión en el ejercicio 2: f(x) = x^3 + x + 1 debe ser (0, 1)
Hola agradecemos tu comentario, tenias razón era un error que ya se corrigió.
la grafica esta mal echa de signos de cada cuadrante
Hola te agradecemos por visitar nuestra pagina, podrías mencionar el número de ejercicio para poder rectificar esos errores que mencionas.
Se podría añadir un poco más de explicación a por que se hace cada paso ( ejemplo porque se divide todo por x ^2?)
Hola agradecemos que puedas darnos tu opinión, cuando surja una duda en este espacio de los comentarios estaremos atentos para darte una explicación con respecto a algo que no entiendas, exista un error o se pueda mejorar una explicación, solo comunícalo y te contestaremos.
Hola, en la parte SIGNOS DE CADA CUADRANTE, esta correcto, en el cuadrante 2 y 4 puede que esté al revés
Hola te agradecemos que visites la pagina, se supone que en el cuadrante 2 los signos (-,+) y en el 4 es (+,-), es así como aparecen?