Capítulos

Definición
La función exponencial es aquella que a cada valor real  le asigna la potencia
le asigna la potencia  con
con  y
y  . Esta función se expresa
. Esta función se expresa

el número  se denomina base.
se denomina base.
Gráficas de funciones exponenciales
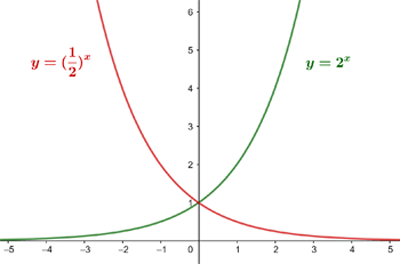
Estudiemos el comportamiento de la función exponencial de acuerdo a su base
Construimos una tabla de valores para 
 |  |
|---|---|
| -3 | 1/8 |
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
Trazamos la gráfica

Ahora construimos una tabla de valores para 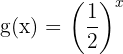
 |  |
|---|---|
| -3 | 8 |
| -2 | 4 |
| -1 | 2 |
| 0 | 1 |
| 1 | 1/2 |
| 2 | 1/4 |
| 3 | 1/8 |
Trazamos la gráfica

Observamos que la primera función es estrictamente creciente, mientras que la segunda es estrictamente decreciente; además ambas son simétricas respecto al eje 
Función exponencial natural
Esta se denota por  donde
donde  está dado por
está dado por
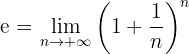
Esta notación fue introducida por Leonhard Euler hacia 1730, al descubrir muchas propiedades de este número. El número  es irracional y sus primeras diez cifras decimales son
es irracional y sus primeras diez cifras decimales son  .
.
Propiedades de la función exponencial
1 Dominio:  .
.
2 Recorrido:  .
.
3 Es continua.
4Los puntos 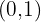 y
y 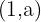 pertenecen a la gráfica.
pertenecen a la gráfica.
5 Es inyectiva 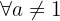 (ninguna imagen tiene más de un original).
(ninguna imagen tiene más de un original).
6 Creciente si 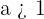 .
.
7 Decreciente si 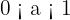 .
.
8 Las curvas  y
y 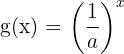 son simétricas respecto al eje
son simétricas respecto al eje  .
.
9 La función exponencial  , con
, con 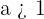 eventualmente crece más rápido que la función potencia
eventualmente crece más rápido que la función potencia  para cualquier
para cualquier  .
.
10 La función inversa de la función exponencial  es
es  . La función inversa de la exponencial natural es
. La función inversa de la exponencial natural es  .
.
Aplicaciones de la función exponencial
Las funciones exponenciales se emplean para modelar una amplia variedad de fenómenos como el crecimiento de poblaciones y las tasas de interés.
Crecimiento y decrecimiento exponencial
La fórmula que se emplea para modelar el crecimiento de una población viene dada por

La función 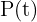 crece exponencialmente y representa la cantidad de la población a tiempo
crece exponencialmente y representa la cantidad de la población a tiempo  ;
;  representa la constante de crecimiento o decrecimiento; si
representa la constante de crecimiento o decrecimiento; si  se llama constante de crecimiento, mientras que si
se llama constante de crecimiento, mientras que si 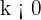 se llama constante de decrecimiento.
se llama constante de decrecimiento. 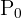 representa la población inicial a tiempo cero, esto es,
representa la población inicial a tiempo cero, esto es, 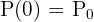 .
.
La fórmula anterior se encuentra expresada en función de la exponencial natural, pero en algunas ocasiones se expresa con base  , esto es sencillo de obtener, basta aplicar las propiedades de los exponentes a
, esto es sencillo de obtener, basta aplicar las propiedades de los exponentes a  y considerar
y considerar 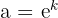 para obtener
para obtener
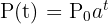
Ejemplo: Un grupo de investigadores estudian un cultivo de bacterias. Si al inicio de la observación se tienen  bacterias y media hora después se tienen
bacterias y media hora después se tienen 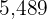 , encuentra:
, encuentra:
1 La cantidad de bacterias al cabo de dos horas.
2 La cantidad de bacterias al cabo de tres horas.
3 La tasa promedio de cambio de la población durante la segunda hora.
4 El tiempo requerido para duplicar la población inicial.
5 ¿Cuándo llegará la población a ser igual a  ?
?
Para poder responder a lo solicitado, primero necesitamos conocer en la fórmula de crecimiento poblacional  con
con 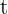 expresado en minutos.
expresado en minutos.
Notamos que conocemos la población inicial  , pero nos falta el valor de la constante de crecimiento. Para encontrar el valor de
, pero nos falta el valor de la constante de crecimiento. Para encontrar el valor de  utilizamos los datos del problema:
utilizamos los datos del problema: 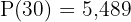 en la fórmula de crecimiento
en la fórmula de crecimiento
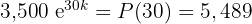
Dividiendo ambos lados por  y aplicando la función inversa de la exponencial natural, se obtiene
y aplicando la función inversa de la exponencial natural, se obtiene

Así la función que modela el crecimiento de la población de bacterias es

1 La cantidad de bacterias al cabo de dos horas es

2 La cantidad de bacterias al cabo de tres horas
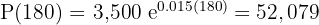
3 La tasa promedio de cambio de la población durante la segunda hora
Durante la segunda hora, el tiempo de  a
a  , la población cambió en
, la población cambió en 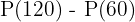 , por lo que la tas promedio en este periodo de tiempo es
, por lo que la tas promedio en este periodo de tiempo es
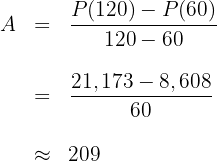
La población aumenta a la tasa promedio aproximada de 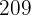 bacterias por minuto durante la segunda hora.
bacterias por minuto durante la segunda hora.
4 El tiempo requerido para duplicar la población inicial
Para esto empleamos la siguiente igualdad
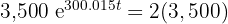
Dividiendo ambos lados por 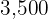 y aplicando la función inversa de la exponencial natural, se obtiene
y aplicando la función inversa de la exponencial natural, se obtiene

Así el tiempo requerido para que la población de bacterias se duplique es 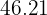 minutos.
minutos.
5 ¿Cuándo llegará la población a ser igual a  ?
?
Para esto empleamos la siguiente igualdad

Dividiendo ambos lados por 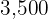 y aplicando la función inversa de la exponencial natural, se obtiene
y aplicando la función inversa de la exponencial natural, se obtiene
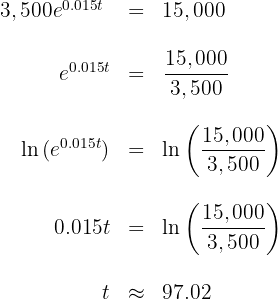
Así el tiempo requerido para que la población de bacterias sea de 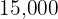 es de
es de 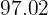 minutos.
minutos.
Interés compuesto
Se invierte una cantidad inicial de dinero 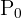 a una tasa de interés
a una tasa de interés  expresada en decimales. Si el interés se capitaliza una sola vez, entonces el saldo a obtener
expresada en decimales. Si el interés se capitaliza una sola vez, entonces el saldo a obtener  después de sumar el interés es
después de sumar el interés es
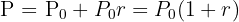
Si el interés se capitaliza más de una vez, el interés que se suma a la cuenta durante un periodo ganará interés durante los periodos siguientes. Si la tasa anual de interés es  y el interés se capitaliza
y el interés se capitaliza  veces por año, entonces al final de
veces por año, entonces al final de  años, el interés se capitalizó
años, el interés se capitalizó 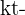 veces y el saldo llamado valor futuro es
veces y el saldo llamado valor futuro es

Ejemplo: Si se invierten  a una tasa de
a una tasa de 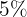 anual. Hallar el valor futuro a
anual. Hallar el valor futuro a  años si el interés es compuesto trimestralmente.
años si el interés es compuesto trimestralmente.
Para encontrar el valor futuro después de  años si el interés se capitaliza trimestralmente, empleamos
años si el interés se capitaliza trimestralmente, empleamos  .
.
Sustituimos los valores en la fórmula del valor futuro
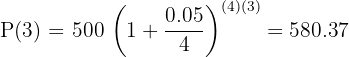
El saldo obtenido después de  años es de
años es de 
Interés compuesto continuamente
Para saber el saldo de una inversión al final de  años cuando la frecuencia de capitalización se incrementa sin límite, esto es, el interés no se capitaliza trimestral, ni mensual, ni diariamente, sino continuamente, se emplea la fórmula
años cuando la frecuencia de capitalización se incrementa sin límite, esto es, el interés no se capitaliza trimestral, ni mensual, ni diariamente, sino continuamente, se emplea la fórmula

Ejemplo: Si se invierten  a una tasa de
a una tasa de 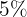 anual. Hallar el valor futuro a
anual. Hallar el valor futuro a  años si el interés es compuesto continuamente.
años si el interés es compuesto continuamente.
Para encontrar el valor futuro después de  años si el interés se capitaliza continuamente, empleamos
años si el interés se capitaliza continuamente, empleamos 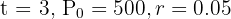 .
.
Sustituimos los valores en la fórmula del valor futuro

El saldo obtenido después de  años es de
años es de 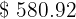 y es el límite superior para el saldo posible.
y es el límite superior para el saldo posible.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Felicitaciones, muy interesantes los problemas y sobretodo las gráficas. ¿Pueden indicarme que programa utilizan?
Hola te agradecemos tu comentario, si te refieres a graficar te recomendamos geogebra, symbolat y otros mas.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
Hola con gusto lo haremos, pero podrías señalar en que ejercicio quieres que lo hagamos, para poder ayudarte.