Capítulos
Las funciones exponenciales son aquellas en las que encontramos a la variable independiente en el exponente, por ejemplo:
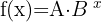
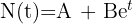
Existen diversos modelos matemáticos que nos permiten describir algunos fenómenos con alguna función exponencial.

Decaimiento radioactivo
En una muestra de un fósil se detectó que el 0.003% del Carbono contenido es Carbono 14 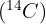 . Si se sabe que el
. Si se sabe que el 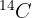 representa el 1% del Carbono presente en un ser vivo y que la vida media del
representa el 1% del Carbono presente en un ser vivo y que la vida media del 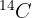 es de 5730 años, ¿Qué tan antiguo es el fósil?
es de 5730 años, ¿Qué tan antiguo es el fósil?
1 Para el decaimiento radiactivo se cumple la siguiente función exponencial
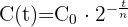
Donde:
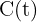 es la cantidad del isotopo radiactivo al tiempo 't'
es la cantidad del isotopo radiactivo al tiempo 't'
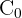 es la cantidad inicial de
es la cantidad inicial de 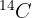 en la muestra
en la muestra
 es la vida media del isotopo radiactivo en años
es la vida media del isotopo radiactivo en años
 es el tiempo transcurrido en años
es el tiempo transcurrido en años
2 Despejamos la variable  de la función exponencial
de la función exponencial
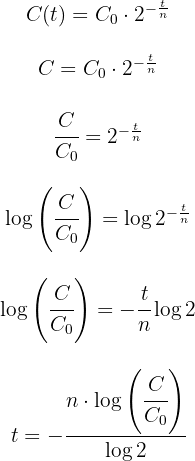
3 Sustituimos los datos y resolvemos las operaciones para obtener el valor de 
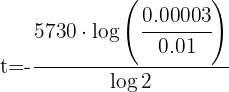
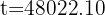
4 El fósil tiene 48022 años de antigüedad
Se sabe que la cantidad de un material radioactivo viene dada por 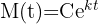 . Si inicialmente hay 100 mg de material y, después de dos años, se observa que el 10% de la masa original se desintegró, encuentra la expresión para la cantidad de masa a tiempo
. Si inicialmente hay 100 mg de material y, después de dos años, se observa que el 10% de la masa original se desintegró, encuentra la expresión para la cantidad de masa a tiempo  .
.
1 Para el decaimiento radiactivo se cumple la siguiente función exponencial
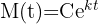
Donde:
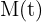 es la cantidad del material radiactivo al tiempo 't'
es la cantidad del material radiactivo al tiempo 't'
 es la cantidad inicial de material radioactivo
es la cantidad inicial de material radioactivo
 es una constante
es una constante
 es el tiempo transcurrido en años
es el tiempo transcurrido en años
2 Despejamos la constante  de la función exponencial
de la función exponencial
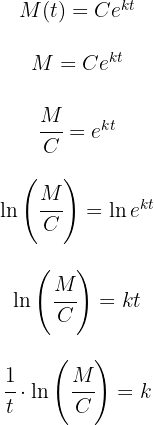
3 Sustituimos los datos y resolvemos las operaciones para obtener el valor de 
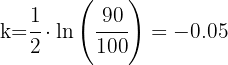
4 La cantidad de material radiactivo a tiempo  es
es 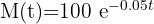
Se sabe que la cantidad de un material radioactivo viene dada por 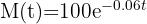 . Si inicialmente hay 100 mg de material, ¿cuánto tiempo se requiere para que se desintegre el 15% del material inicial?
. Si inicialmente hay 100 mg de material, ¿cuánto tiempo se requiere para que se desintegre el 15% del material inicial?
1 Para el decaimiento radiactivo se cumple la siguiente función exponencial
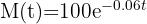
2 Despejamos el tiempo  de la función exponencial
de la función exponencial
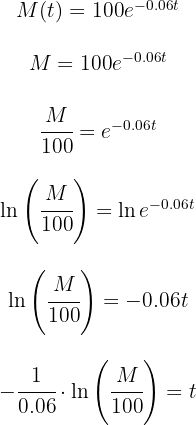
3 Sustituimos los datos y resolvemos las operaciones para obtener el valor de 
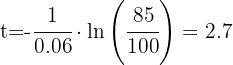 años
años
Se sabe que la cantidad de un material radioactivo viene dada por 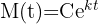 . Encuentra la expresión para la vida media del material radioactivo.
. Encuentra la expresión para la vida media del material radioactivo.
1 Para el decaimiento radiactivo se cumple la siguiente función exponencial
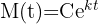
Donde:
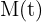 es la cantidad del material radiactivo al tiempo 't'
es la cantidad del material radiactivo al tiempo 't'
 es la cantidad inicial de material radioactivo
es la cantidad inicial de material radioactivo
 es una constante
es una constante
 es el tiempo transcurrido en años
es el tiempo transcurrido en años
 es la cantidad media de material, esto es, la mitad de la cantidad inicial
es la cantidad media de material, esto es, la mitad de la cantidad inicial
2 Sustituimos la cantidad media del material y para encontrar la vida media, despejamos el tiempo  de la función exponencial
de la función exponencial
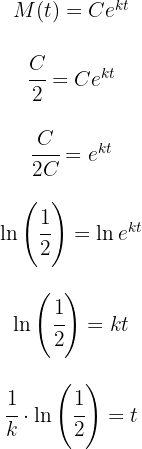
3 Así, la vida media para el material radioactivo es
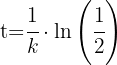
Un material radioactivo se desintegra un tercio en 200 años. Determina su vida media.
1 Para el decaimiento radiactivo se cumple la siguiente función exponencial
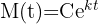
Donde:
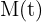 es la cantidad del material radiactivo al tiempo 't'
es la cantidad del material radiactivo al tiempo 't'
 es la cantidad inicial de material radioactivo
es la cantidad inicial de material radioactivo
 es una constante
es una constante
 es el tiempo transcurrido en años
es el tiempo transcurrido en años
2 Despejamos la constante  de la función exponencial
de la función exponencial
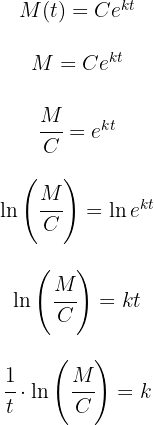
3 Sustituimos para obtener el valor de la constante k
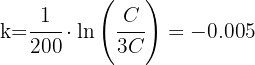
4 Así, la vida media para el material radioactivo es
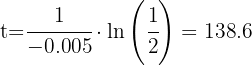 años
años
Crecimiento poblacional
Una población de bacterias crece de acuerdo a la función 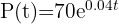 , donde el tiempo
, donde el tiempo  está dado en horas. ¿Cuántas bacterias habrá después de 5 horas?
está dado en horas. ¿Cuántas bacterias habrá después de 5 horas?
1 Como tenemos la función de población solamente en términos del tiempo, sustituimos 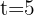
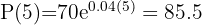
2 Así, 5 horas después habrá 85 bacterias.
Una población de bacterias crece de acuerdo a la función 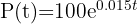 , donde el tiempo
, donde el tiempo  está dado en minutos. ¿Cuánto tiempo debe transcurrir para que hayan 15000 bacterias?
está dado en minutos. ¿Cuánto tiempo debe transcurrir para que hayan 15000 bacterias?
1 Primero despejaremos 't'
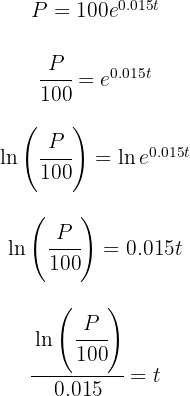
2 Sustituimos los datos obtenidos para calcular el valor de 't'
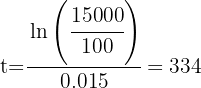
3 Debe transcurrir 334 minutos o 5 horas con 34 minutos para que la población sea de 15000 bacterias
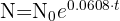
Una población de bacterias crece de acuerdo a la función 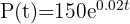 , donde el tiempo
, donde el tiempo  está dado en minutos. ¿Cuántas bacterias habrá después de 1.5 horas?
está dado en minutos. ¿Cuántas bacterias habrá después de 1.5 horas?
1 Como tenemos la función de población solamente en términos del tiempo, sustituimos 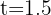 horas que es igual 90 minutos
horas que es igual 90 minutos
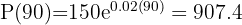
2 Así, 1.5 horas después habrá 907 bacterias.
Sabemos que la cantidad, 'N', de insectos en 't' años está dada por una función exponencial del tipo 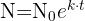 . Un grupo de biólogos estimó que la población creció en 20% durante los últimos 3 años y saben que si la población crece en un 70% con respecto a la población original se convertiría en una plaga. ¿En cuántos años se estima que la población de insectos se convierta en una plaga?
. Un grupo de biólogos estimó que la población creció en 20% durante los últimos 3 años y saben que si la población crece en un 70% con respecto a la población original se convertiría en una plaga. ¿En cuántos años se estima que la población de insectos se convierta en una plaga?
1 Como no conocemos el valor de la constante 'k' debemos utilizar los datos que nos dan para obtenerla. Así que primero despejaremos 'k'
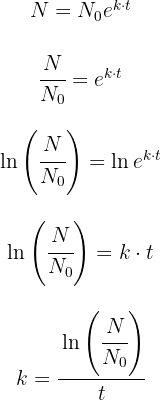
2 Sustituimos los datos obtenidos para calcular el valor de 'k'
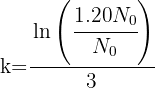
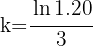
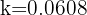
3 La función exponencial nos queda como
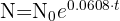
4 Despejamos la variable 't'
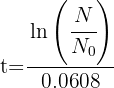
5 Sustituimos la condición 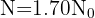 y resolvemos
y resolvemos
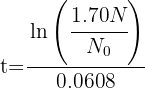
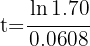
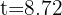
6 La población crecerá en 70% a los 8.72 años
El crecimiento de la población humana puede describirse mediante una función de crecimiento logístico. Para la población de una isla caribeña se sabe que se ajusta a la función 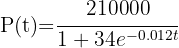 y
y  corresponde a la población que había en la isla en el año 2000.
corresponde a la población que había en la isla en el año 2000.
a ¿Cuántos habitantes habrá en 2025?
b ¿En cuántos años se duplicará la población con respecto a la que había en 2020?
a ¿Cuántos habitantes habrá en 2025?
1 Sustituimos 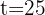 en la función y resolvemos
en la función y resolvemos
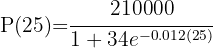
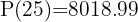
b ¿En cuántos años se duplicará la población con respecto a la que había en el 2000?
1 Calculamos 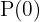
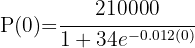
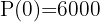
2 Despejamos la variable 't'
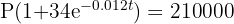
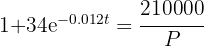
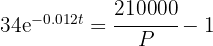
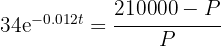
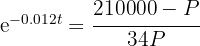
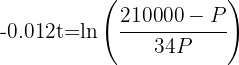
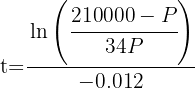
3 Sustituimos 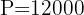
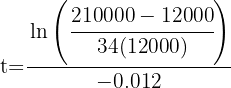
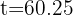
4 La población se duplicará durante el año 2060, aproximadamente.
Ley de enfriamiento de Newton
Se calienta agua hasta alcanzar una temperatura de 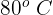 y se deja enfriar en unentorno frio. Si la función que describe la temperatura del agua es
y se deja enfriar en unentorno frio. Si la función que describe la temperatura del agua es 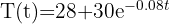 , con el tiempo dado en minutos; ¿qué temperatura tendrá a los 10 minutos?
, con el tiempo dado en minutos; ¿qué temperatura tendrá a los 10 minutos?
1 Sustituimos los datos conocidos en la ecuación de temperatura
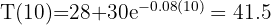
2 Así, el agua tendrá una temperatura de 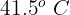
Pedro saca del horno un pan que tiene una temperatura de 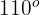 . Si la función de que mide la temperatura es
. Si la función de que mide la temperatura es 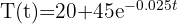 , donde 't' está medido en minutos, ¿cuál es la temperatura del pan a los 15 minutos de salir del horno?
, donde 't' está medido en minutos, ¿cuál es la temperatura del pan a los 15 minutos de salir del horno?
1 Sustituimos los datos conocidos en la ecuación de temperatura
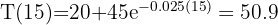
2 Así, el pan tendrá una temperatura de 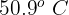
Un objeto metálico marca una temperatura de 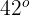 . Si la función de que mide la temperatura es
. Si la función de que mide la temperatura es 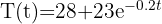 , donde 't' está medido en minutos y 28 representa la temperatura del ambiente. ¿En cuánto tiempo el objeto tendrá una temperatura de 30 grados?
, donde 't' está medido en minutos y 28 representa la temperatura del ambiente. ¿En cuánto tiempo el objeto tendrá una temperatura de 30 grados?
1 Despejamos el tiempo 't' y sustituimos los datos cuando 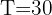
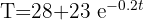
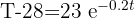
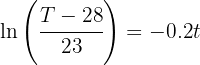
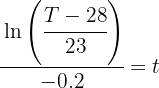
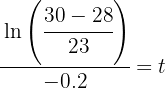
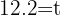
2 Así, el objeto tardará 12.2 minutos en alcanzar la temperatura de 30 grados
Una taza de café después de prepararse marca una temperatura de 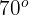 . Si la función de que mide la temperatura es
. Si la función de que mide la temperatura es 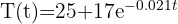 , donde 't' está medido en minutos y 25 representa la temperatura del ambiente. ¿En cuánto tiempo la taza de café tendrá una temperatura de 40 grados?
, donde 't' está medido en minutos y 25 representa la temperatura del ambiente. ¿En cuánto tiempo la taza de café tendrá una temperatura de 40 grados?
1 Despejamos el tiempo 't' y sustituimos los datos cuando 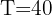
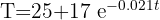
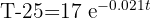
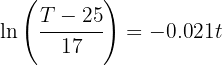
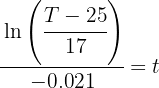

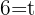
2 Así, la taza de café tardará 6 minutos en alcanzar la temperatura de 40 grados
La temperatura corporal de una persona es de 37 ºC. Se sabe que cuando una persona fallece, en promedio tarda 20 horas para que su temperatura corporal llegue a 27ºC si la temperatura del medio ambiente permanece a 25ºC. Si el cuerpo humano cumple con la Ley de enfriamiento de Newton:
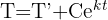
Siendo T, la temperatura a las 't' horas y T' la temperatura del ambiente.
Un médico forense observa que la temperatura de una persona que falleció es de 29ºC y la temperatura ambiente se mantuvo a 25ºC desde el fallecimiento. Si el reloj del médico marca las 7:00pm, ¿A qué hora se estima el fallecimiento?
1 Con los datos que nos da el problema podemos calcular el valor de las constantes 'C' y 'k'. Primero, evaluemos la ecuación en 
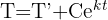
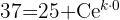
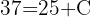
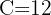
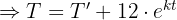
2 Despejamos la constante 'k' y sustituimos los datos cuando 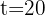
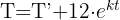
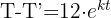
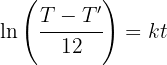
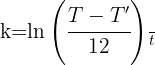
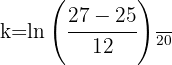
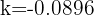
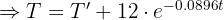
3 De la función resultante despejamos a 't' y sustituimos los datos cuando 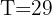
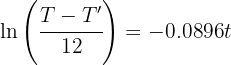
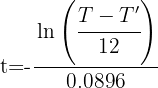
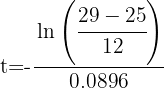
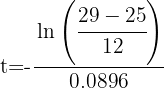
Han pasado alrededor de 12.26 horas
4 La persona falleció un poco antes de las 7:00am
Interés compuesto
María invierte 900 euros a una tasa de interés anual de 5%. ¿Cuál será su capital después de 2 años?
1 La fórmula para calcular el interés compuesto es
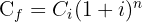
2 Sustituimos los datos para calcular el capital final
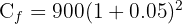
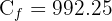
Pedro invierte 850 euros a una tasa de interés anual de 6%. ¿En cuánto tiempo tendrá 1000 euros?
1 Despejamos la variable 'n' de la función
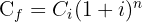
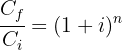
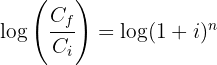
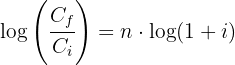
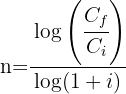
2 Sustituimos los datos para obtener el valor de 'n'
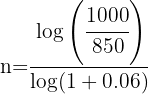
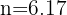
3 Se requieren más de 6 años para que el capital ascienda a 5000 euros
Se invierte 400 euros y al cabo de 2 años se obtiene 500 euros. ¿Cuál es la tasa de interés anual?
1 Despejamos la variable 'i' de la función
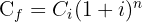
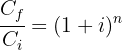
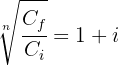
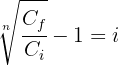
2 Sustituimos los datos para obtener el valor de 'i'
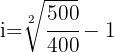
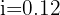
3 Así, la tasa de interés es de 12% anual
Se invierte 981 euros y al cabo de 3 años se obtiene 1200 euros. ¿Cuál es la tasa de interés anual?
1 Despejamos la variable 'i' de la función
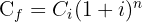
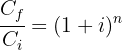
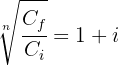
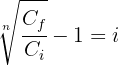
2 Sustituimos los datos para obtener el valor de 'i'
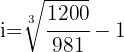
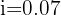
3 Así, la tasa de interés es de 7% anual
Una persona invierte un capital de 3200 euros en un banco que le ofrece una tasa de interés anual del 7.5%
a ¿A cuánto ascendería su capital en 3 años?
b ¿En cuántos años tendría un capital de 5000 euros?
a¿A cuánto ascendería su capital en 3 años?
1 La fórmula para calcular el interés compuesto es
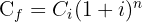
2 Sustituimos los datos para calcular el capital final
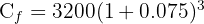
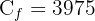
3 En 3 años, el capital ascenderá a 3975 euros
b ¿En cuántos años tendría un capital de 5000 euros?
1 Despejamos la variable 'n' de la función
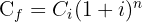
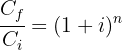
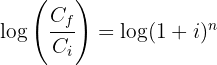
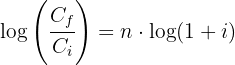
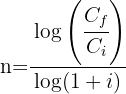
2 Sustituimos los datos para obtener el valor de 'n'
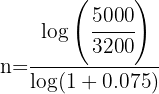
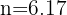
3 Se requieren más de 6 años para que el capital ascienda a 5000 euros
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
Hola con gusto lo haremos, pero podrías señalar en que ejercicio quieres que lo hagamos, para poder ayudarte.
Podrían mostrar los pares ordenados para graficarlo, gracias