Capítulos
- Dominio de la función polinómica entera
- Dominio de la función racional
- Dominio de la función radical de índice impar
- Dominio de la función radical de índice par
- Dominio de la función logarítmica
- Dominio de la función exponencial
- Dominio de la función seno
- Dominio de la función coseno
- Dominio de la función tangente
- Dominio de la función cotangente
- Dominio de la función secante
- Dominio de la función cosecante
- Dominio de operaciones con funciones
El dominio de una función está formado por todos los elementos que tienen imagen.
Es decir, son los valores de  que podemos sustituir en la regla de correspondencia de una función para obtener el valor correspondiente de
que podemos sustituir en la regla de correspondencia de una función para obtener el valor correspondiente de  .
.

que significa que el dominio de una función son aquellos valores de  que pertenecen a los números reales para los cuales existe un valor asociado de la función
que pertenecen a los números reales para los cuales existe un valor asociado de la función  .
.
El subconjunto de los números reales en el que se define la función se llama dominio o campo existencia de la función.
Se designa por D.
La variable x perteneciente al dominio de la función recibe el nombre de variable independiente.

Conjunto inicial Conjunto final
Dominio Conjunto imagen o recorrido

Dominio de la función polinómica entera
El dominio de una función polinómica es  , porque cualquier número real tiene imagen.
, porque cualquier número real tiene imagen.
También son funciones polinómicas enteras las que tienen un número (una constante) en el denominador:
Ejemplos de dominios de las funciones polinómicas
1 

2 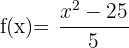

Puedes probar que al sustituir cualquier valor de  en las funciones siempre obtendrás un valor correspondiente para
en las funciones siempre obtendrás un valor correspondiente para  .
.
Dominio de la función racional
El dominio es  menos los valores que anulan al denominador (no puede existir una fracción cuyo denominador sea cero)..
menos los valores que anulan al denominador (no puede existir una fracción cuyo denominador sea cero)..
Ejemplo de ejercicio de dominio de la función racional
1 ¿Qual es el dominio de la función 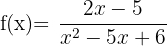 ?
?
Igualamos el denominador a  y resolvemos la ecuación
y resolvemos la ecuación

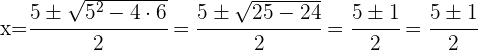



Dominio de la función radical de índice impar
El dominio es el dominio de la función radicando.
1

2

Dominio de la función radical de índice par
El dominio está formado por todos los valores del radicando que hacen que éste sea mayor o igual que cero.
1




2



3¿Cuál es el dominio de la función ?
?
En este caso, el denominador debe ser mayor que cero y, además, debemos buscar los valores de  para que la raíz exista, por lo que:
para que la raíz exista, por lo que:




4Determinar el dominio de la función  .
.
El radicando tiene que ser mayor que cero y el denominador distinto de cero



5 Obtener el dominio de la función  .
.
Como el radicando debe ser mayor o igual que cero, planteamos la desigualdad:

Resolvemos la inecuación de segundo grado


Las raíces de la ecuación de segundo grado asociada a la desigualdad son:  y
y 
Por lo que los intervalos en los que se cumple la desigualdad serían:

El dominio lo forman los valores menores que el -2 y mayores que 7, incluyéndolos.

6 Obtener el dominio de la función 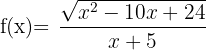 .
.
En este caso se deben cumplir dos condiciones, una para el cociente y otra para la raíz, por lo que el numerador tiene que ser mayor o igual que cero y el denominador distinto de cero. Por lo que:




Dominio de la función logarítmica
El dominio está formado por todos los valores que hacen que la función que aparece dentro del logaritmo sea mayor que cero.

Se debe cumplir:




Dominio de la función exponencial
Ejemplos de dominio de funciones exponenciales
1 

2 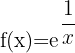
El dominio es igual a  menos los valores que anulan el denominador del exponente
menos los valores que anulan el denominador del exponente

3 
El dominio coincide con el campo de existencia real de la raíz

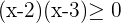



Dominio de la función seno
El dominio de la función seno es 
Dominio de la función coseno
El dominio de la función coseno es 
Dominio de la función tangente


Dominio de la función cotangente


Dominio de la función secante


Dominio de la función cosecante


Dominio de operaciones con funciones

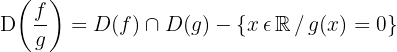




Recuerda que también puedes encontrar un profesor particular para cursos de matematicas adaptados a tu nivel.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
El Punto de inflexión en el ejercicio 2: f(x) = x^3 + x + 1 debe ser (0, 1)
Hola agradecemos tu comentario, tenias razón era un error que ya se corrigió.
la grafica esta mal echa de signos de cada cuadrante
Hola te agradecemos por visitar nuestra pagina, podrías mencionar el número de ejercicio para poder rectificar esos errores que mencionas.
Se podría añadir un poco más de explicación a por que se hace cada paso ( ejemplo porque se divide todo por x ^2?)
Hola agradecemos que puedas darnos tu opinión, cuando surja una duda en este espacio de los comentarios estaremos atentos para darte una explicación con respecto a algo que no entiendas, exista un error o se pueda mejorar una explicación, solo comunícalo y te contestaremos.